NME cv 18.02..2019

Contents

operace s maticemi

+, /, *, /, magic(N), zeros(N), ones(N), eye(N) (pozn. diagonalni) zmena M,N /teho prvku v ni MTX(M,N) = cislo

N = 3;
pridany_radek = [2 2 3];
pridany_sloupec = [3 3 2]';
MTX1 = magic(3);
MTX2 = [MTX1, pridany_sloupec];
MTX3 = [MTX1; pridany_radek];

reseni soustavy Ax=b

A = magic (3);
b = [5 5 5]';
x = A\b;    %vysledek

indexace

%od jednicky !!!

% posledni prvek index 'end'
v = [1 2 3 4 5];
v(end)
v(end+1) = 0;   %prida do vektoru v na konec nulu

ans =

     5

logicke operatory

pro napr ruzne podminky : >, <, >=, <=, ==, ~= (pozn. nerovnitko)

historie v cmd window

FIND - hledani pozice prvku

MTX4 = [ 8 1 -2; 3 4 6; -3 0 7];
find (MTX4 < 0)     % vraci indexy prvku v matici MTX4, mensich nez 0

ans =

     3
     7

uklid

komentare CTRL+T clc, clear, clear all, close all,...

%otevrit editor - edit

Cvicny skript

a = 5;
if a > 3
    disp('a je vetsi nez 3')
else
    disp('a je mensi nez 3')
end

a je vetsi nez 3

prace s fcemi -> soubor fce

cykly

for, while, ... break, continue

%switch, case, otherwise

switch a
    case 1
        hlaska = 'a je 1';
    case 2
        hlaska = 'a je 2';
    otherwise
        hlaska = 'a je neco jineho';
end

(pseudo-) nahodna cisla

rand
randn   %normalni rovnomerne rozdeleni (mezi 0 a 1)
MTXrandom = rand(3)    %generuje i matice
round(10*MTXrandom) %round(10*rand(3))   %zaokrouhluji desetinasobek predchozi matice

ans =

    0.8147


ans =

   -0.4326


MTXrandom =

    0.9058    0.6324    0.5469
    0.1270    0.0975    0.9575
    0.9134    0.2785    0.9649


ans =

     9     6     5
     1     1    10
     9     3    10

grafy a vystupy

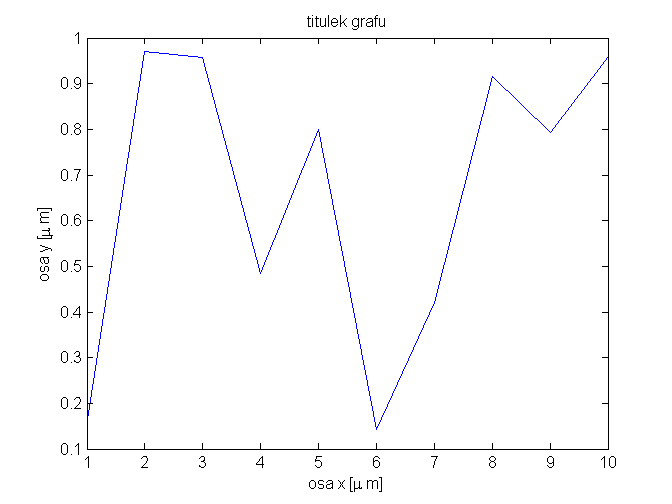
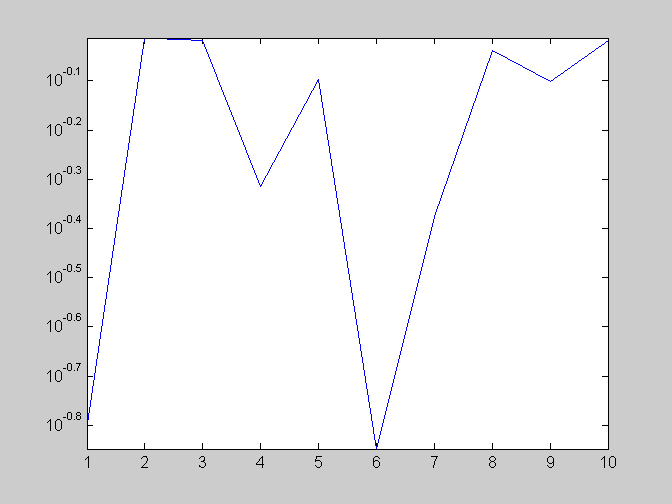
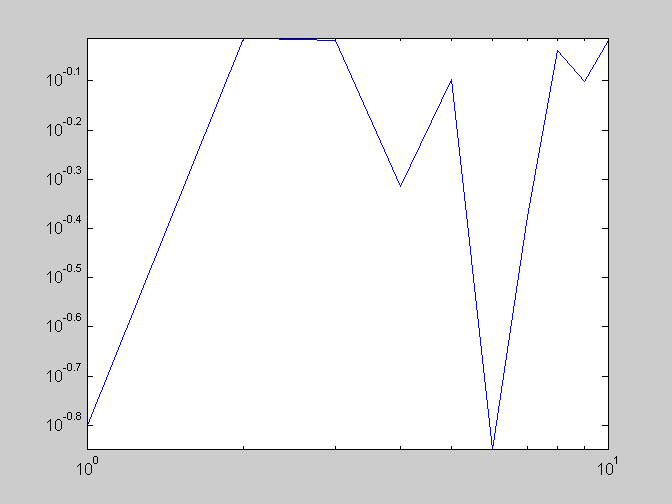
figure(1)
x = 1:10
y = rand(1, 10)
plot(x,y)   %jednoduchy, klasicky, linearni graf
xlabel('osa x [\mu m]') %funguje LaTeXova sazba pismenek (viz obr)
ylabel('osa y [\mu m]')
title('titulek grafu')
figure(2)
semilogy(x,y)   %osa y je logaritmicka
figure(3)
loglog(x,y) %obe osy maji logaritmicky prubeh

cislo = 5;
sprintf('zde je trxtovy vystup jako v C ... \n cisilko pet -> %d ', cislo)  % %d umisti cislo, odsazeni \n

x =

     1     2     3     4     5     6     7     8     9    10


y =

    0.1576    0.9706    0.9572    0.4854    0.8003    0.1419    0.4218    0.9157    0.7922    0.9595


ans =

zde je trxtovy vystup jako v C ... 
 cisilko pet -> 5 

'statisticke' operatory

min(y)
max(y)
min(min(MTX1))  %global
max(max(MTX1))  %global

ans =

    0.1419


ans =

    0.9706


ans =

     1


ans =

     9

Published with MATLAB® 7.5