Jacobiho metoda reseni soustav rovnic

NME cv , 11.03.2019.

pozor na znaceni L,U : nejde o LU-dekompozici (neni tu nasobeni jako v ni, ale scitani)

popis metody (co-jak-proc) hledej ve skriptech

K rozdeleni matice A na horni a dolni trojuhelnikovou matici vyuzijeme built-in fce MATLABu > fce tril a triu (dolni a horni) pozn. prip. lze snadno do-implementovat pomoci FOR cyklu...

pocatecni deklarace vstupu
vypocet pro matici A
vypocet pro matici B
vykres RESENI pro matici A a B (prevzato)
vykres CHYBY pro matici A a B (prevzato)

pocatecni deklarace vstupu

A = [5 1 1; 2 7 3; 2 3 8]   % zalezi na PD matic (poc.podm.)
B = [5 10 1; 2 7 3; 2 3 8]

y = [1; 1; 1] %sloupcova prava strana

x_puvodni_odhad = [1; 2; 3]

pocet_iteraci = 100;
x = x_puvodni_odhad;

A =

     5     1     1
     2     7     3
     2     3     8


B =

     5    10     1
     2     7     3
     2     3     8


y =

     1
     1
     1


x_puvodni_odhad =

     1
     2
     3

vypocet pro matici A

L = tril (A, -1);
U = triu(A, 1);

D = A - L - U;  %diag matice, na diagonale ma diagonalni prvky puvodni matice A

F = -inv(D) * (L + U);  % predpisy jsou dany ve skriptech
G = inv(D);

reseni_A = A\y; %reseni primou metodou v MATLABu pro porovnani a vypocet chyby

for i=1:pocet_iteraci
    x = F * x + G * y;
    velikost_reseni_A (i) = norm(x);
    velikost_chyby_A (i) = norm( x - reseni_A );
end

vypocet pro matici B

poyor, ted si prepisuji spoustu promennych, ktere driv byly pro matici A, realnymi daty z matice B!!!!

L = tril (B, -1);
U = triu(B, 1);

D = B - L - U;  %diag matice, na diagonale ma diagonalni prvky puvodni matice A

F = -inv(D) * (L + U);  % predpisy jsou dany ve skriptech
G = inv(D);

reseni_B = B\y; %reseni primou metodou v MATLABu pro porovnani a vypocet chyby

for i=1:pocet_iteraci
    x = F * x + G * y;
    velikost_reseni_B (i) = norm(x);
    velikost_chyby_B (i) = norm( x - reseni_B );
end

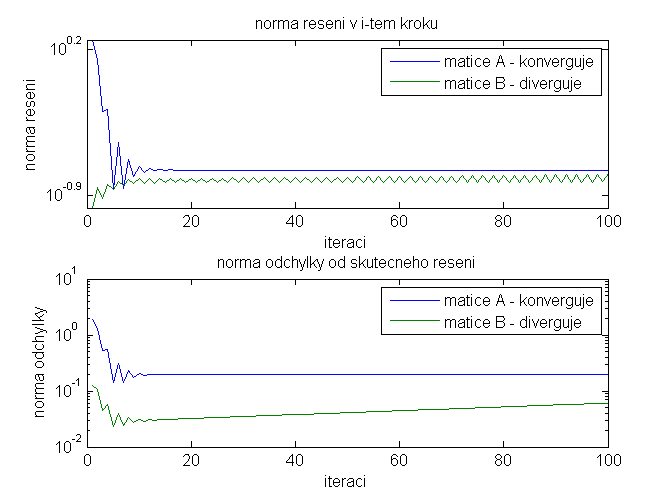
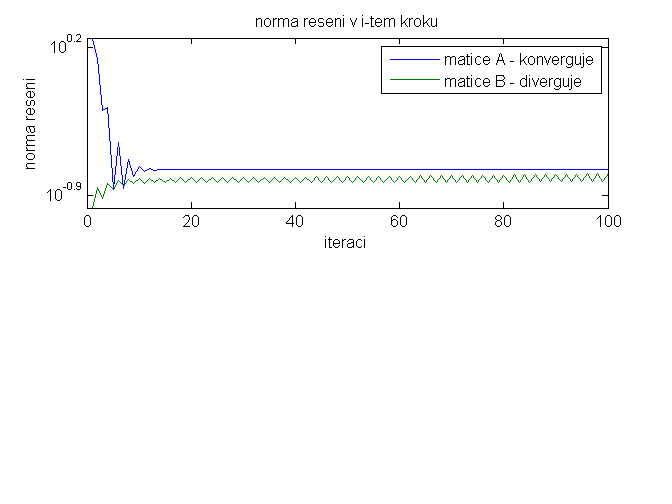
vykres RESENI pro matici A a B (prevzato)

subplot(211);
plot(1:pocet_iteraci, velikost_reseni_A, 1:pocet_iteraci, velikost_reseni_B);
title('norma reseni v i-tem kroku');
xlabel('iteraci');
ylabel('norma reseni');
legend('matice A - konverguje','matice B - diverguje');
set(gca,'YScale','log');

vykres CHYBY pro matici A a B (prevzato)

subplot(212);
plot(1:pocet_iteraci, velikost_reseni_A, 1:pocet_iteraci, velikost_chyby_B);
title('norma odchylky od skutecneho reseni');
xlabel('iteraci');
ylabel('norma odchylky');
legend('matice A - konverguje','matice B - diverguje');
set(gca,'YScale','log');